计算点
使用说明
在网关内部,计算点是对采集数据的二次逻辑加工计算过程,是采集点的有力补充;
不同型号的网关,其计算点上限数量从128 ~ 1024不等,请参照设备规格说明书。
计算点的定义是遵循程序表达式的样式,特别类似C 语言或turbo C语言的语法;不仅支持简单的四则运算、函数计算、逻辑计算,还支持自定义变量,数组,循环,逻辑分支流程,微分,微积分;详情示例见下文描述。
计算点的定义
如果计算点是简单的函数表达式,按照C 语言的函数表达式进行计算公式定义,配置软件的页面点击左侧的”配置 -> 边缘计算”, 填写计算点名称/描述,添加引用采集点名称。如下截图:
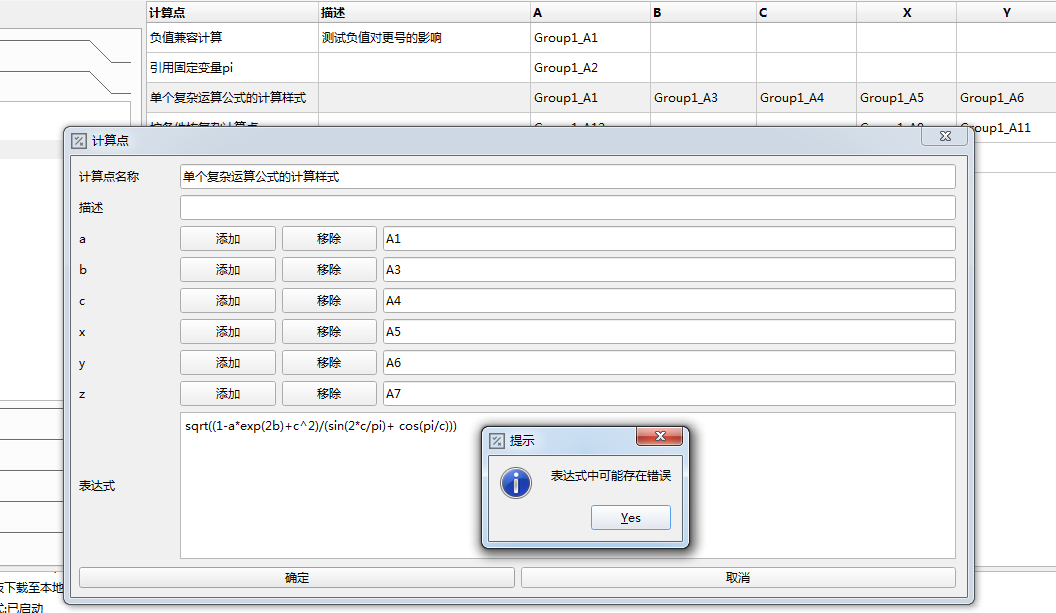
注意:为了避免采集点的冗长复杂的名称,表达式中将把采集点的值简化成a,b,c,x,y,z这6个变量;在撰写计算点表达式时不要再重复定义这6个变量名称,以免混淆而产生不可预测的计算结果。
完成编辑之后,点击确定,配置软件会进行初步效验,给出的建议可以忽略。
计算点公式转换
如果计算点表达式含有逻辑分支与判断,也可以定义程序分支;目前支持if-then-else,switch等逻辑分支; 表达式也支持while,for 等简单循环控制。如下截图
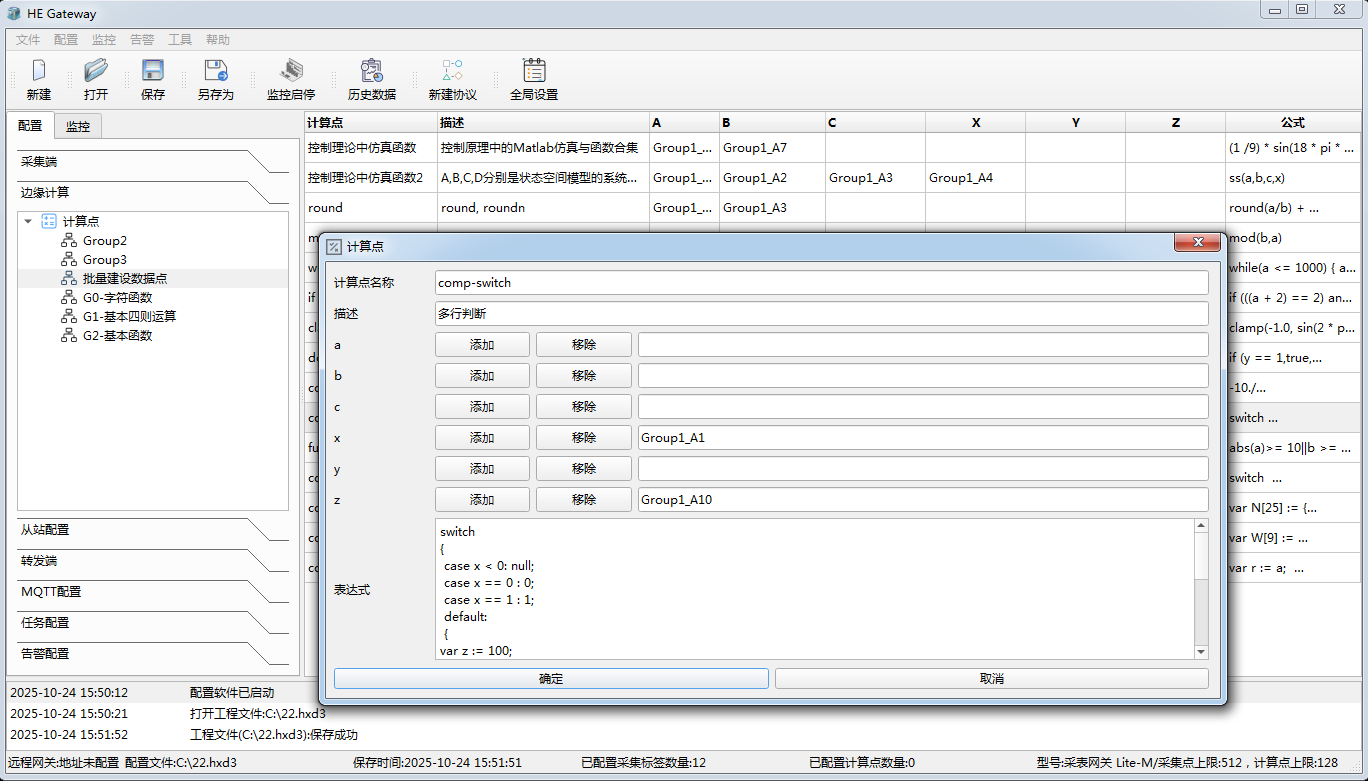
计算点的跟踪
在配置文件上传到指定网关,系统会立即重启运行;在配置工具中,可以通过监控模式进行跟踪。
支持的列表
| 类型 | 内容 |
|---|---|
| 基本运算符 | +, -, *, /, %, ^ |
| 复合运算 | =, +=, -=, *=, /=, %= |
| 相等判断 | =, ==, <>, !=, <, <=, >, >= |
| 逻辑运算符 | and, mand, mor, nand, nor, not, or, shl, shr,xnor, xor, true, false |
| 函数 | abs, avg, ceil, clamp, equal, erf, erfc, exp, expm1, floor, frac, log, log10, log1p, log2, logn, max, min, mul, ncdf, not_equal, root, round, roundn, sgn, sqrt, sum, swap, trunc |
| 三角学 | acos, acosh, asin, asinh, atan, atanh, atan2, cos, cosh, cot, csc, sec, sin, sinc, sinh, tan, tanh, hypot, rad2deg, deg2grad, deg2rad,grad2deg |
| 控制结构 | if-then-else, 三元条件语句, switch-case,return语句 |
| 循环语句 | while, for, repeat-until, break, continue |
| 微积分 | 数值积分与微分 |
简单示例
(01) sqrt(1 - (3 / x^2))
(02) clamp(-1, sin(2 * pi * x) + cos(y / 2 * pi), +1)
(03) sin(2.34e-3 * x)
(04) if(((x[2] + 2) == 3) and ((y + 5) <= 9), 1 + w, 2 / z)
(05) inrange(-2, m, +2) == if(({-2 <= m} and [m <= +2]), 1, 0)
(06) ({1/1}*[1/2]+(1/3)) - {1/4}^[1/5]+(1/6) - ({1/7}+[1/8]*(1/9))
(07) a * exp(2.2 / 3.3 * t) + c
(08) z := x + sin(2.567 * pi / y)
(09) u := 2.123 * {pi * z} / (w := x + cos(y / pi))
(10) 2x + 3y + 4z + 5w == 2 * x + 3 * y + 4 * z + 5 * w
(11) 3(x + y) / 2.9 + 1.234e+12 == 3 * (x + y) / 2.9 + 1.234e+12
(12) (x + y)3.3 + 1 / 4.5 == [x + y] * 3.3 + 1 / 4.5
(13) (x + y[i])z + 1.1 / 2.7 == (x + y[i]) * z + 1.1 / 2.7
(14) (sin(x / pi) cos(2y) + 1) == (sin(x / pi) * cos(2 * y) + 1)
(15) 75x^17 + 25.1x^5 - 35x^4 - 15.2x^3 + 40x^2 - 15.3x + 1
(16) (avg(x,y) <= x + y ? x - y : x * y) + 2.345 * pi / x
(17) while (x <= 100) { x -= 1; }
(18) sgn(+1.2^3.4z / -5.6y) <= {-7.8^9 / -10.11x }
基础详细示例
算术运算符和赋值运算符
| 运算符 | 表达式 | 解释 |
|---|---|---|
| + | x + y | x和y之间的加法 |
| - | x - y | x和y之间的减法 |
| * | x * y | x和y之间的乘法 |
| / | x / y | x和y之间的除法 |
| % | x % y | x相对于y的模 |
| ^ | x ^ y | x的y次方 |
| := | y := x | 将x的值赋给y,其中y是变量或向量类型。 |
| += | x += abs(y - z) | 按右侧表达式的值递增x。其中x是变量或向量类型。 |
| -= | x[i] -= abs(y + z) | 将x减去右侧表达式的值。其中x是变量或向量类型。 |
| *= | x *= abs(y / z) | 将x乘以右侧表达式的值赋给x。其中x是变量或向量类型。 |
| /= | x[i + j] /= abs(y * z) | 将x除以右侧表达式的值指定为x。其中x是变量或向量类型。 |
| %= | x[2] %= y ^ 2 | 将右侧表达式的值取模x赋值给x。其中x是变量或向量类型。 |
相等与不相等
| 运算符 | 表达式 | 解释 |
|---|---|---|
== 或= |
x == y |
x 等于 y |
!= 或 <> |
x != y |
x 不等于 y |
< |
x < y |
x 小于 y |
<= |
x <= y |
x 小于等于 y |
> |
x > y |
x 大于 y |
| >= | x >= y x >= y |
x 大于等于 y |
布尔运算
| 运算符 | 表达式 | 解释 |
|---|---|---|
true |
真实状态或除零以外的任何值(通常为1) | |
false |
假(值为 0) | |
and |
x and y |
逻辑与,只有当x和y都为真时才为真 |
mand |
mand(x > y, z < w, u or v, w and x |
多输入逻辑AND,仅当所有输入均为真时为真。表达式从左向右短路。 |
mor |
mor(x > y, z < w, u or v, w and x |
多输入逻辑OR,如果至少有一个输入为真,则为真。表达式从左向右短路。 |
nand |
x nand y |
逻辑NAND,仅当x或y为假时为真 |
nor |
x nor y |
逻辑NOR,仅当x或y的结果为假时为真 |
not |
not(x and y |
逻辑非,否定输入的逻辑意义 |
or |
x or y |
逻辑OR,如果x或y为真,则为真 |
xor |
x xor y |
逻辑XOR,仅当x和y的逻辑状态不同时为真 |
xnor |
x xnor y |
当满足x和y的双条件时,逻辑XNOR为真 |
& |
(x & y) == (y and x) |
类似于AND,但具有从左到右的表达式短路优化 |
| | | (x | y) == (y or x) | 类似于AND,但具有从左到右的表达式短路优化 |
通用函数
| 函数名 | 表达式 | 解释 |
|---|---|---|
| abs | abs(x) |
绝对值 |
| avg | avg(x,y,z,w,u,v) == (x + y + z + w + u + v) / 6) |
所有输入的平均值。 |
ceil |
大于或等于x的最小整数 | |
clamp |
clamp(r0,x,r1 |
夹紧x在r0和r1之间的范围内,其中r0<r1 |
equal |
使用归一化epsilon进行x和y之间的等式检验 | |
erf |
erf(x) |
x的误差函数 |
erfc |
erfc(x) |
x的免费错误功能 |
exp |
exp(x) |
e是x的幂 |
expm1 |
expm1(x) |
e是x的幂减去1,其中x非常小 |
floor |
floor(x) |
小于或等于x的最大整数 |
frac |
frac(x) |
x 的小数部分 |
hypot |
hypot(x,y)= sqrt(xx + yy) |
x和y的张力减退 |
iclamp |
iclamp(r0,x,r1) |
反向箝位x在r0和r1范围之外。其中r0<r1。如果x在范围内,它将捕捉到最接近的界限。 |
inrange |
inrange(r0,x,r1) |
当x在r0和r1的范围内时,In range返回“true”。其中r0<r1 |
log |
log(x) |
x的自然对数 |
log10 |
log10(x) |
以10为底的x对数 |
log1p |
log1p(x) |
1+x的自然对数,其中x非常小 |
log2 |
log2(x) |
以2为底的x的对数 |
logn |
logn(x,8) |
以N为底的x的对数,其中N为正整数。 |
max |
max(x,y,z,w,u,v) |
所有输入中的最大值 |
min |
min(x,y,z,w,u) |
所有输入中的最小值 |
mul |
mul(x,y,z,w,u,v,tt) == (x y z w u v t) |
所有输入的乘积 |
ncdf |
ncdf(x) |
正态累积分布函数 |
not_equal |
使用归一化epsilon对x和y进行不等检验 | |
pow |
pow(x,y) == x ^ y |
x是y的幂 |
root |
root(x,3) == x^(1/3) |
x的n次根,其中n为正整数 |
round |
round(x) |
将x四舍五入到最接近的整数 |
roundn |
roundn(x,3)roundn(1.2345678,4) == 1.2346 |
将x四舍五入到n位小数 |
sgn |
sgn(x) |
x的符号,当x<0时为-1,当x>0时为+1,否则为零 |
sqrt |
sqrt(x) |
x的平方根,其中x>=0 |
sum |
sum(x,y,z,w,u,v,t) == (x + y + z + w + u + v + t) |
所有输入的总和 |
swap <=> |
swap(x,y) or x <=> y |
交换变量x和y的值,并返回y的当前值 |
trunc |
trunc(x) |
x 的整数部分 |
三角函数
| 函数名 | 表达式 | 解释 |
|---|---|---|
acos |
acos(x) |
以弧度表示的x的弧余弦。间隔[-1,+1] |
acosh |
acosh(x) |
以弧度表示的x的反双曲余弦 |
asin |
asin(x) |
x的正弦弧,以弧度表示。间隔[-1,+1] |
asinh |
asinh(x) |
以弧度表示的x的反双曲正弦 |
atan |
atan(x) |
x的反正切,以弧度表示。间隔[-1,+1] |
atan2 |
atan2(x,y) | (x/y)的反正切,以弧度表示。[-pi,+pi] |
atanh |
atanh(x) |
以弧度表示的x的反双曲正切 |
cos |
cos(x) |
x的余弦。 |
cosh |
cosh(x) |
x的双曲余弦 |
cot |
cot(x) |
x的转折点 |
csc |
csc(x) |
x的余音 |
sec |
`sec(x) | x秘书 |
sin |
sin(x) |
x的正弦 |
sinc |
sinc(x) |
x的正弦基数 |
sinh |
sinh(x) |
x的双曲正弦 |
tan |
tan(x) |
x切线 |
tanh |
tanh(x) |
x的双曲正切 |
deg2rad |
deg2rad(x) |
将x从度数转换为弧度 |
deg2grad |
deg2grad(x) |
将x从度数转换为gradians |
rad2deg |
rad2deg(x) |
将x从弧度转换为度数 |
grad2deg |
grad2deg(x) |
将x从gradians转换为度数 |
控制流程语句
| 语句 | 表达式 | 解释 |
|---|---|---|
if |
1. if (x, y, z) 2. if ((x + 1) > 2y, z + 1, w / v) 3. if (x > y) z; 4. if (x <= 2*y) { z + w } |
如果x为真,则返回y,否则返回z |
if-else |
1. if (x > y) z; else w; 2. if (x > y) z; else if (w != u) v; 3. if (x < y) { z; w + 1; } else u; 4. if ((x != y) and (z > w)) { y := sin(x) / u; z := w + 1; } else if (x > (z + 1)) { w := abs (x - y) + z; u := (x + 1) > 2y ? 2u : 3u; } |
if else/else if语句。根据条件分支,语句将返回结果分支或替代分支的值。 |
switch |
switch { case x > (y + z) : 2 * x / abs(y - z); case x < 3 : sin(x + y); default : 1 + x; } |
遇到的第一个真实情况将决定切换的结果。 如果所有情况条件都不成立,则默认操作被假定为最终返回值。这有时也被称为多路分支机制。 |
while |
while ((x -= 1) > 0) { y := x + z; w := u + y; } |
当条件为真时,该结构将重复评估内部语句。 最终迭代中的最终语句应作为循环的返回值 |
| repeat/until | repeat y := x + z; w := u + y; until ((x += 1) > 100) |
该结构将反复评估内部语句,“直到”条件为真。最终迭代中的最终语句应作为循环的返回值 |
for |
for (var x := 0; (x < n) and (x != y); x += 1) { y := y + x / 2 - z; w := u + y; } |
当条件为真时,该结构将重复评估内部语句。 在每次循环迭代中,都会计算一个“递增”表达式。 条件是必需的,而初始化器和递增表达式是可选的 |
break |
while ((i += 1) < 10) { if (i < 5) j -= i + 2; else if (i % 2 == 0) break; else break[2i + 3]; } |
Break终止最近的封闭Break循环的执行,允许在循环外部继续执行。 默认的break语句将循环的返回值设置为NaN,而基于返回的表单将该值设置为break表达式的值 |
continue |
for (var i := 0; i < 10; i += 1) { if (i < 5) continue; j -= i + 2; } |
继续将跳过最近封闭环体的剩余部分 |
return |
1. return [1]; 2. return [x, 'abx']; 3. return [x, x + y,'abx']; 4. return []; 5. if (x < y) return [x, x - y, 'result-set1', 123.456]; else return [y, x + y, 'result-set2'] |
立即从当前表达式中返回。可以选择传回可变数量的值(标量、向量或字符串) |
?: |
1. x ? y : z 2. x + 1 > 2y ? z + 1 : (w / v) 3. min(x,y) > z ? (x < y + 1) ? x : y : (w * v) |
三元条件语句,类似于上述if语句 |
~ |
~(i := x + 1, j := y / z, k := sin(w/u)) == (sin(w/u))) ~{i := x + 1; j := y / z; k := sin(w/u)} == (sin(w/u))) |
计算每个子表达式,然后返回最后一个子表达式的值作为结果。 这有时被称为多序列点评估 |
| [*] | [*] { case (x + 1) > (y - 2) : x := z / 2 + sin(y / pi); case (x + 2) < abs(y + 3) : w / 4 + min(5y,9); case (x + 3) == (y * 4) : y := abs(z / 6) + 7y; } |
评估其案例陈述为真的任何结果。 返回值要么为零,要么为最后一个被评估的结果 |
| [] | 1. v[] 2. max_size := max(v0[],v1[],v2[],v3[]) |
向量大小运算符返回正在操作的向量的大小 |
位运算函数
| 函数名 | 表达式 | 解释 |
|---|---|---|
| shl | shl(a,2) | 将a左移2位,等同a<<2 |
| shr | shr(a,2) | 将a右移2位,等同a>>2 |
案例:
例子1:单个复杂运算公式的表达式
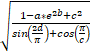 = sqrt((1-a*exp(2b)+c^2)/(sin(2*c/pi)+ cos(pi/c)))
= sqrt((1-a*exp(2b)+c^2)/(sin(2*c/pi)+ cos(pi/c)))
例子2:定义变量及逻辑判断语句
switch {
case x < 0: null;
case x == 0 : 0;
case x == 1 : 1;
default:{
var z := 100;
var sqrt_x := x / 2;
repeat
if (equal(sqrt_x^2, x))
break[sqrt_x];
else
sqrt_x := (1 / 2) * (sqrt_x + (x / sqrt_x));
until ((z -= 1) <= 0);
};
}
例子3:少量变量,复杂的判断条件的表达式
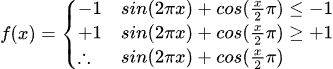
clamp(-1.0, sin(2 * pi * x) + cos(x / 2 * pi), +1.0)
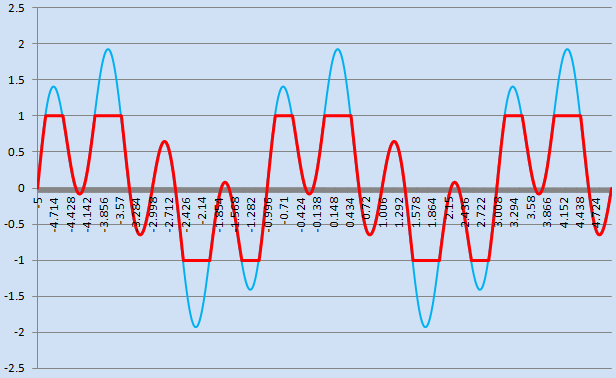
例子4:循环导致系统卡顿,计算点无值
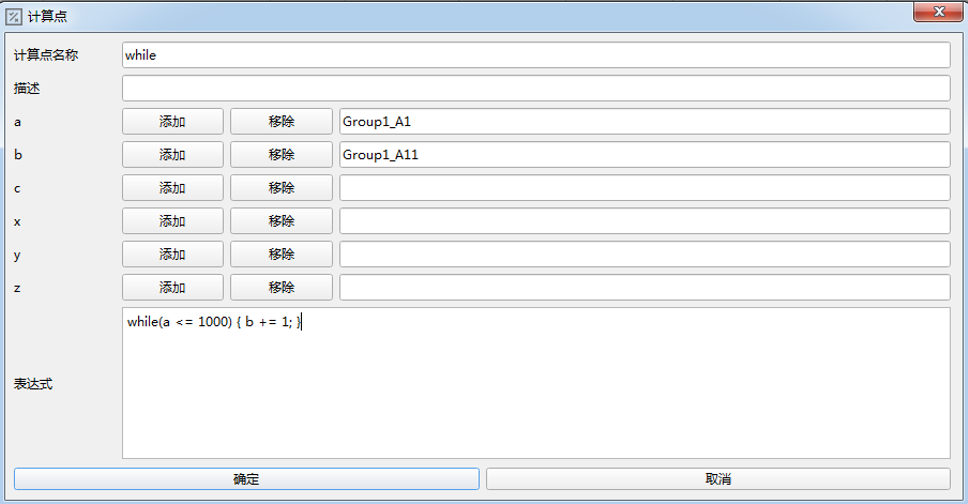
注意:如果书写循环,请注意一定不能写成死循环,死循环表达式会导致系统卡顿,采集点、计算点无数据,网关响应慢;解决方法就是纠正表达式,重新上传配置文件。
如下语句就会导致异常循环:while(a <= 1000) (b += 1) ,在该表达式中:a是恒小于1000的值,条件恒定为true,所以就产生了死循环。
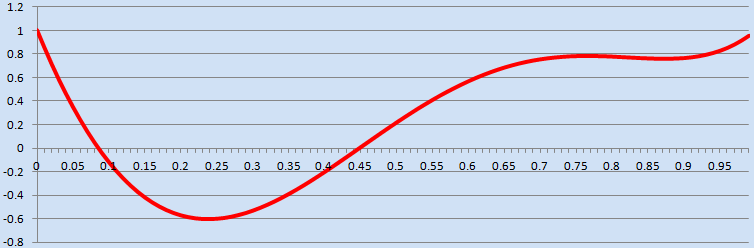
例子4:带有隐乘法多项式求值
25x^5 - 35x^4 - 15x^3 + 40x^2 - 15x + 1
例子5:矢量处理方法的标准偏差
var k[25] := {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25};
sqrt(sum([k - avg(k)]^2) / k[])*a